165680 Two capacitors, each having capacitance $40 \mu \mathrm{F}$ are connected in series. The space between one of the capacitors is filled with dielectric material of dielectric constant $K$ such that the equivalence capacitance of the system became $24 \mu \mathrm{F}$. The value of $\mathrm{K}$ will be :
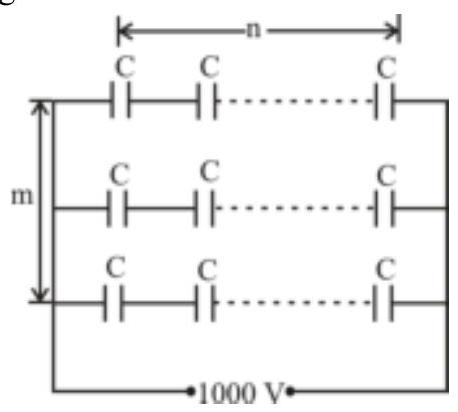
165682 An electric circuit requires a total capacitance of $2 \mu \mathrm{F}$ across a potential of $1000 \mathrm{~V}$. Large number of $1 \mu \mathrm{F}$ capacitances are available each of which would breakdown if the potential is more than $350 \mathrm{~V}$. How many capacitances are required to make the circuit?
165680 Two capacitors, each having capacitance $40 \mu \mathrm{F}$ are connected in series. The space between one of the capacitors is filled with dielectric material of dielectric constant $K$ such that the equivalence capacitance of the system became $24 \mu \mathrm{F}$. The value of $\mathrm{K}$ will be :
165682 An electric circuit requires a total capacitance of $2 \mu \mathrm{F}$ across a potential of $1000 \mathrm{~V}$. Large number of $1 \mu \mathrm{F}$ capacitances are available each of which would breakdown if the potential is more than $350 \mathrm{~V}$. How many capacitances are required to make the circuit?
165680 Two capacitors, each having capacitance $40 \mu \mathrm{F}$ are connected in series. The space between one of the capacitors is filled with dielectric material of dielectric constant $K$ such that the equivalence capacitance of the system became $24 \mu \mathrm{F}$. The value of $\mathrm{K}$ will be :
165682 An electric circuit requires a total capacitance of $2 \mu \mathrm{F}$ across a potential of $1000 \mathrm{~V}$. Large number of $1 \mu \mathrm{F}$ capacitances are available each of which would breakdown if the potential is more than $350 \mathrm{~V}$. How many capacitances are required to make the circuit?
165680 Two capacitors, each having capacitance $40 \mu \mathrm{F}$ are connected in series. The space between one of the capacitors is filled with dielectric material of dielectric constant $K$ such that the equivalence capacitance of the system became $24 \mu \mathrm{F}$. The value of $\mathrm{K}$ will be :
165682 An electric circuit requires a total capacitance of $2 \mu \mathrm{F}$ across a potential of $1000 \mathrm{~V}$. Large number of $1 \mu \mathrm{F}$ capacitances are available each of which would breakdown if the potential is more than $350 \mathrm{~V}$. How many capacitances are required to make the circuit?