165589 The distance between two plates of a capacitor is $d$ and its capacitance is $C_{1}$, when air is the medium between the plates. If a metal sheet of thickness $\frac{2 d}{3}$ and of same area as plate is introduced between the plates, the capacitance of the capacitor becomes $C_{2}$. The ratio $\frac{C_{2}}{C_{1}}$ is:

165591 A big drop of radius $R$ is formed by 729 small drops of water of radius $r$, then the radius of each small drop will be:

165592 The earth is assumed to be a charged conducting sphere having volume ' $V$ ' and surface area ' $A$ '. The capacitance of the earth in free space is
( $\varepsilon_{0}=$ permittivity of free space)

165594 Assume each oil drop consists of a capacitance of $C$. If combine $n$ drops to form a bigger drop, then the capacitance of bigger drop $C^{\prime}$ would be

165596 A capacitor of capacitance $10 \mu \mathrm{F}$ is charged to potential $50 \mathrm{~V}$ with a battery. The battery is now disconnected and an additional charge $200 \mu \mathrm{C}$ is given to the positive plate of the capacitor. The potential difference across the capacitor will be

165589 The distance between two plates of a capacitor is $d$ and its capacitance is $C_{1}$, when air is the medium between the plates. If a metal sheet of thickness $\frac{2 d}{3}$ and of same area as plate is introduced between the plates, the capacitance of the capacitor becomes $C_{2}$. The ratio $\frac{C_{2}}{C_{1}}$ is:

165591 A big drop of radius $R$ is formed by 729 small drops of water of radius $r$, then the radius of each small drop will be:

165592 The earth is assumed to be a charged conducting sphere having volume ' $V$ ' and surface area ' $A$ '. The capacitance of the earth in free space is
( $\varepsilon_{0}=$ permittivity of free space)

165594 Assume each oil drop consists of a capacitance of $C$. If combine $n$ drops to form a bigger drop, then the capacitance of bigger drop $C^{\prime}$ would be

165596 A capacitor of capacitance $10 \mu \mathrm{F}$ is charged to potential $50 \mathrm{~V}$ with a battery. The battery is now disconnected and an additional charge $200 \mu \mathrm{C}$ is given to the positive plate of the capacitor. The potential difference across the capacitor will be

165589 The distance between two plates of a capacitor is $d$ and its capacitance is $C_{1}$, when air is the medium between the plates. If a metal sheet of thickness $\frac{2 d}{3}$ and of same area as plate is introduced between the plates, the capacitance of the capacitor becomes $C_{2}$. The ratio $\frac{C_{2}}{C_{1}}$ is:

165591 A big drop of radius $R$ is formed by 729 small drops of water of radius $r$, then the radius of each small drop will be:

165592 The earth is assumed to be a charged conducting sphere having volume ' $V$ ' and surface area ' $A$ '. The capacitance of the earth in free space is
( $\varepsilon_{0}=$ permittivity of free space)

165594 Assume each oil drop consists of a capacitance of $C$. If combine $n$ drops to form a bigger drop, then the capacitance of bigger drop $C^{\prime}$ would be

165596 A capacitor of capacitance $10 \mu \mathrm{F}$ is charged to potential $50 \mathrm{~V}$ with a battery. The battery is now disconnected and an additional charge $200 \mu \mathrm{C}$ is given to the positive plate of the capacitor. The potential difference across the capacitor will be

165589 The distance between two plates of a capacitor is $d$ and its capacitance is $C_{1}$, when air is the medium between the plates. If a metal sheet of thickness $\frac{2 d}{3}$ and of same area as plate is introduced between the plates, the capacitance of the capacitor becomes $C_{2}$. The ratio $\frac{C_{2}}{C_{1}}$ is:

165591 A big drop of radius $R$ is formed by 729 small drops of water of radius $r$, then the radius of each small drop will be:

165592 The earth is assumed to be a charged conducting sphere having volume ' $V$ ' and surface area ' $A$ '. The capacitance of the earth in free space is
( $\varepsilon_{0}=$ permittivity of free space)

165594 Assume each oil drop consists of a capacitance of $C$. If combine $n$ drops to form a bigger drop, then the capacitance of bigger drop $C^{\prime}$ would be

165596 A capacitor of capacitance $10 \mu \mathrm{F}$ is charged to potential $50 \mathrm{~V}$ with a battery. The battery is now disconnected and an additional charge $200 \mu \mathrm{C}$ is given to the positive plate of the capacitor. The potential difference across the capacitor will be

165589 The distance between two plates of a capacitor is $d$ and its capacitance is $C_{1}$, when air is the medium between the plates. If a metal sheet of thickness $\frac{2 d}{3}$ and of same area as plate is introduced between the plates, the capacitance of the capacitor becomes $C_{2}$. The ratio $\frac{C_{2}}{C_{1}}$ is:

165591 A big drop of radius $R$ is formed by 729 small drops of water of radius $r$, then the radius of each small drop will be:

165592 The earth is assumed to be a charged conducting sphere having volume ' $V$ ' and surface area ' $A$ '. The capacitance of the earth in free space is
( $\varepsilon_{0}=$ permittivity of free space)

165594 Assume each oil drop consists of a capacitance of $C$. If combine $n$ drops to form a bigger drop, then the capacitance of bigger drop $C^{\prime}$ would be

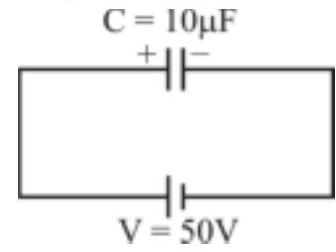
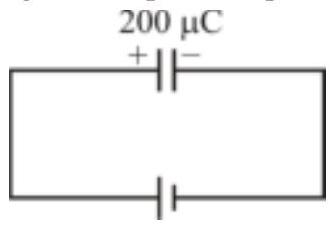
165596 A capacitor of capacitance $10 \mu \mathrm{F}$ is charged to potential $50 \mathrm{~V}$ with a battery. The battery is now disconnected and an additional charge $200 \mu \mathrm{C}$ is given to the positive plate of the capacitor. The potential difference across the capacitor will be