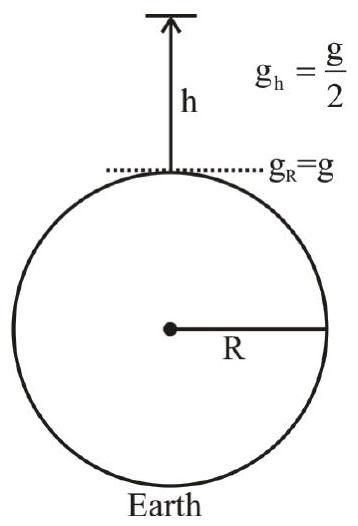
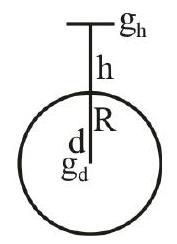
138323
Find the acceleration of our galaxy, due to the nearest comparably sized galaxy. The approximate masses of each galaxy is $8 \times 10^{11}$ solar mass and they are separated by 2 million light-years. Each galaxy has a diameter of 100000 light year.
(Assume, 1 light year $\approx 10^{16} \mathrm{~m}$, gravitational constant, $G \approx 10^{-10}\left(\frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}\right)$ and mass of sun $\left.=2.0 \times 10^{30} \mathrm{~kg}\right)$
138323
Find the acceleration of our galaxy, due to the nearest comparably sized galaxy. The approximate masses of each galaxy is $8 \times 10^{11}$ solar mass and they are separated by 2 million light-years. Each galaxy has a diameter of 100000 light year.
(Assume, 1 light year $\approx 10^{16} \mathrm{~m}$, gravitational constant, $G \approx 10^{-10}\left(\frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}\right)$ and mass of sun $\left.=2.0 \times 10^{30} \mathrm{~kg}\right)$
138323
Find the acceleration of our galaxy, due to the nearest comparably sized galaxy. The approximate masses of each galaxy is $8 \times 10^{11}$ solar mass and they are separated by 2 million light-years. Each galaxy has a diameter of 100000 light year.
(Assume, 1 light year $\approx 10^{16} \mathrm{~m}$, gravitational constant, $G \approx 10^{-10}\left(\frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}\right)$ and mass of sun $\left.=2.0 \times 10^{30} \mathrm{~kg}\right)$
138323
Find the acceleration of our galaxy, due to the nearest comparably sized galaxy. The approximate masses of each galaxy is $8 \times 10^{11}$ solar mass and they are separated by 2 million light-years. Each galaxy has a diameter of 100000 light year.
(Assume, 1 light year $\approx 10^{16} \mathrm{~m}$, gravitational constant, $G \approx 10^{-10}\left(\frac{\mathrm{Nm}^{2}}{\mathrm{~kg}^{2}}\right)$ and mass of sun $\left.=2.0 \times 10^{30} \mathrm{~kg}\right)$