138241
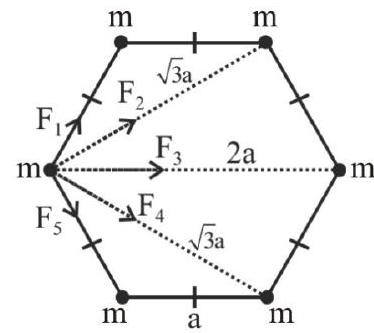
A uniform sphere of mass $M$ and radius $R$ exerts a force $F$ on a small mass $m$ situated at a distance of $2 R$ from the centre $O$ of the sphere. A spherical portion of diameter $R$ is cut from the sphere as shown in figure. The force of attraction between the remaining part of the sphere and the mass $m$ will be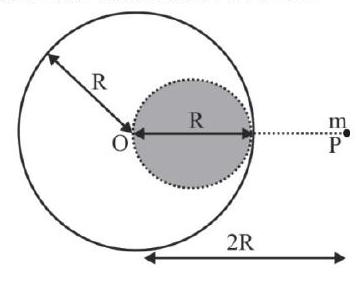
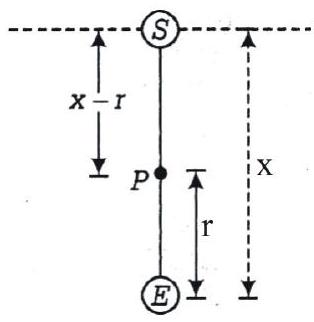
138247 A rocket is fired from the Earth towards the Sun. At what distance from the Earth's centre, the gravitational force on the rocket is zero? Mass of the Sun $=2 \times 10^{30} \mathrm{~kg}$ and mass of the Earth $=6 \times 10^{24} \mathrm{~kg}$. Neglect the effect of other planets etc. $\left(\right.$ orbital radius $=1.5 \times 10^{11} \mathrm{~m}$ )
138241
A uniform sphere of mass $M$ and radius $R$ exerts a force $F$ on a small mass $m$ situated at a distance of $2 R$ from the centre $O$ of the sphere. A spherical portion of diameter $R$ is cut from the sphere as shown in figure. The force of attraction between the remaining part of the sphere and the mass $m$ will be
138247 A rocket is fired from the Earth towards the Sun. At what distance from the Earth's centre, the gravitational force on the rocket is zero? Mass of the Sun $=2 \times 10^{30} \mathrm{~kg}$ and mass of the Earth $=6 \times 10^{24} \mathrm{~kg}$. Neglect the effect of other planets etc. $\left(\right.$ orbital radius $=1.5 \times 10^{11} \mathrm{~m}$ )
138241
A uniform sphere of mass $M$ and radius $R$ exerts a force $F$ on a small mass $m$ situated at a distance of $2 R$ from the centre $O$ of the sphere. A spherical portion of diameter $R$ is cut from the sphere as shown in figure. The force of attraction between the remaining part of the sphere and the mass $m$ will be
138247 A rocket is fired from the Earth towards the Sun. At what distance from the Earth's centre, the gravitational force on the rocket is zero? Mass of the Sun $=2 \times 10^{30} \mathrm{~kg}$ and mass of the Earth $=6 \times 10^{24} \mathrm{~kg}$. Neglect the effect of other planets etc. $\left(\right.$ orbital radius $=1.5 \times 10^{11} \mathrm{~m}$ )
138241
A uniform sphere of mass $M$ and radius $R$ exerts a force $F$ on a small mass $m$ situated at a distance of $2 R$ from the centre $O$ of the sphere. A spherical portion of diameter $R$ is cut from the sphere as shown in figure. The force of attraction between the remaining part of the sphere and the mass $m$ will be
138247 A rocket is fired from the Earth towards the Sun. At what distance from the Earth's centre, the gravitational force on the rocket is zero? Mass of the Sun $=2 \times 10^{30} \mathrm{~kg}$ and mass of the Earth $=6 \times 10^{24} \mathrm{~kg}$. Neglect the effect of other planets etc. $\left(\right.$ orbital radius $=1.5 \times 10^{11} \mathrm{~m}$ )