269586 An initial momentum is imparted to a homogeneous cylinder, as a result of which it begins to roll without slipping up an inclined plane at a speed of \(\mathrm{v}_{0}=4 \mathrm{~m} / \mathrm{sec}\) The plane makes an angle \(\theta=30^{\circ}\) with the horizontal. What height \(h\) will the cylinder rise to? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
269587 A solid cylinder starts rolling down on an inclined plane from its top and \(\mathrm{V}\) is velocity of its centre of mass on reaching the bottom of inclined plane. If a block starts sliding down on an identical inclined plane but smooth, from its top, then the velocity of block on reaching the bottom of inclined plane is
269588
A wheel of radius \(0.2 \mathrm{~m}\) rolls without slip ping with a speed \(10 \mathrm{~m} / \mathrm{s}\) on a horizontal road. When it is at a point \(A\) on the road, a small lump of mud separates from the wheel at its highest point \(B\) and drops at point \(C\) on the ground. The distance \(A C\) is
269586 An initial momentum is imparted to a homogeneous cylinder, as a result of which it begins to roll without slipping up an inclined plane at a speed of \(\mathrm{v}_{0}=4 \mathrm{~m} / \mathrm{sec}\) The plane makes an angle \(\theta=30^{\circ}\) with the horizontal. What height \(h\) will the cylinder rise to? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
269587 A solid cylinder starts rolling down on an inclined plane from its top and \(\mathrm{V}\) is velocity of its centre of mass on reaching the bottom of inclined plane. If a block starts sliding down on an identical inclined plane but smooth, from its top, then the velocity of block on reaching the bottom of inclined plane is
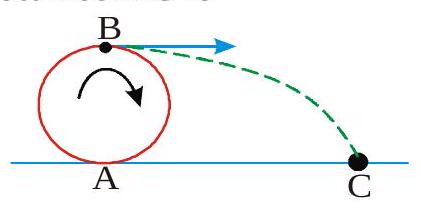
269588
A wheel of radius \(0.2 \mathrm{~m}\) rolls without slip ping with a speed \(10 \mathrm{~m} / \mathrm{s}\) on a horizontal road. When it is at a point \(A\) on the road, a small lump of mud separates from the wheel at its highest point \(B\) and drops at point \(C\) on the ground. The distance \(A C\) is

269586 An initial momentum is imparted to a homogeneous cylinder, as a result of which it begins to roll without slipping up an inclined plane at a speed of \(\mathrm{v}_{0}=4 \mathrm{~m} / \mathrm{sec}\) The plane makes an angle \(\theta=30^{\circ}\) with the horizontal. What height \(h\) will the cylinder rise to? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
269587 A solid cylinder starts rolling down on an inclined plane from its top and \(\mathrm{V}\) is velocity of its centre of mass on reaching the bottom of inclined plane. If a block starts sliding down on an identical inclined plane but smooth, from its top, then the velocity of block on reaching the bottom of inclined plane is
269588
A wheel of radius \(0.2 \mathrm{~m}\) rolls without slip ping with a speed \(10 \mathrm{~m} / \mathrm{s}\) on a horizontal road. When it is at a point \(A\) on the road, a small lump of mud separates from the wheel at its highest point \(B\) and drops at point \(C\) on the ground. The distance \(A C\) is

269586 An initial momentum is imparted to a homogeneous cylinder, as a result of which it begins to roll without slipping up an inclined plane at a speed of \(\mathrm{v}_{0}=4 \mathrm{~m} / \mathrm{sec}\) The plane makes an angle \(\theta=30^{\circ}\) with the horizontal. What height \(h\) will the cylinder rise to? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
269587 A solid cylinder starts rolling down on an inclined plane from its top and \(\mathrm{V}\) is velocity of its centre of mass on reaching the bottom of inclined plane. If a block starts sliding down on an identical inclined plane but smooth, from its top, then the velocity of block on reaching the bottom of inclined plane is
269588
A wheel of radius \(0.2 \mathrm{~m}\) rolls without slip ping with a speed \(10 \mathrm{~m} / \mathrm{s}\) on a horizontal road. When it is at a point \(A\) on the road, a small lump of mud separates from the wheel at its highest point \(B\) and drops at point \(C\) on the ground. The distance \(A C\) is

269586 An initial momentum is imparted to a homogeneous cylinder, as a result of which it begins to roll without slipping up an inclined plane at a speed of \(\mathrm{v}_{0}=4 \mathrm{~m} / \mathrm{sec}\) The plane makes an angle \(\theta=30^{\circ}\) with the horizontal. What height \(h\) will the cylinder rise to? \(\left(g=10 \mathrm{~m} / \mathrm{s}^{2}\right)\)
269587 A solid cylinder starts rolling down on an inclined plane from its top and \(\mathrm{V}\) is velocity of its centre of mass on reaching the bottom of inclined plane. If a block starts sliding down on an identical inclined plane but smooth, from its top, then the velocity of block on reaching the bottom of inclined plane is
269588
A wheel of radius \(0.2 \mathrm{~m}\) rolls without slip ping with a speed \(10 \mathrm{~m} / \mathrm{s}\) on a horizontal road. When it is at a point \(A\) on the road, a small lump of mud separates from the wheel at its highest point \(B\) and drops at point \(C\) on the ground. The distance \(A C\) is

